Bekijk onderstaande grafiek. We gaan de formule bepalen, die bij lijn l hoort.



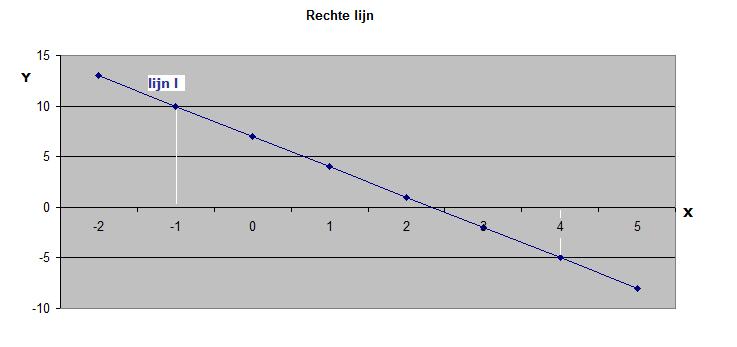
Duidelijke punten zijn (-1,) en (4,).

Om de formule van lijn l te bepalen gaan we uit van de algemene formule van een rechte lijn: y = a·x + b, waarbij we de getallen a en b nog nader moeten bepalen.

Het getal a is de helling (met een duur woord de richtingscoëfficient) van de lijn.
Je kunt de helling bepalen door de verandering van y te delen door de verandering van x:



Voor bovenstaande grafiek geldt:
de verandering van y = -15 (de grafiek daalt);
de verandering van x = +5.

De helling is dus -15 : 5 = -3.
Het getal a in de formule y = a·x + b is hiermee bepaald.
a =

Het getal b is het begingetal, oftewel: de waarde van y bij het punt x=0.
Uit de grafiek lees je af dat bij het punt x = 0 de waarde y = +7 hoort (0,7).
Het getal b in de formule y = a·x + b is hiermee bepaald.
b=

De formule die bij lijn l hoort, wordt: y = ·x +

Het probleem is opgelost: je hebt de formule bepaald die hoort bij bovenstaande lineaire grafiek!

Ter controle kun je enkele x-waarden invullen:
x = -1 y = -3·-1 + 7 = 10 (klopt met de grafiek).
x = 0 y = -3·0 + 7 = 7 (klopt ook met de grafiek).